Traveling Queen STEM

1.Definition of the n-Queens Problem

In a chess newspaper in 1848, Max Bezzel asks the question, can eight queens be placed on a standard chessboard so that no queen may attack another? This is the rst known instance of a non-attacking queens puzzle being posed. The problem was quickly solved by Franz Nauck who published the entire list of 92 solutions on the 8 x 8 chessboard in 1850. Nauck also asked a more general question, now known as the n-queens problem, that has inspired so much interest.

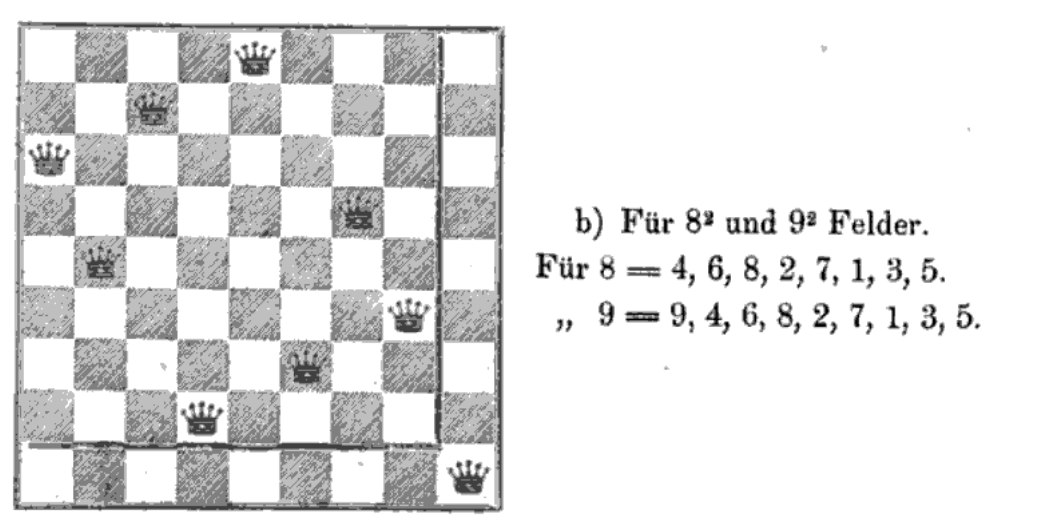
In a pair of articles published in 1874, E. Pauls gives a solution set of arrangements of n-queens for all $n>3$ . Some examples from his paper appear below, and one can see that Pauls makes use of the fact that any two queens who are positioned a knight’s move apart are independent of each other. Pauls also completes the proof that Nauck’s list of solutions is complete.

While we now know that $n$ -queens may always be arranged on the board for any $n>3$ , the harder question is, how many ways can we arrange a set of non-attacking queens for each $n$ . The answer to this question is still unknown! Computers and brute force methods have identified the counts for low values of $n$ , that is for $1\leq n \leq 27$ . We provide the first few values below, but the Online Encyclopedia of Integer Sequences contains a complete list of values.

Over time many variations to the n-queens problem have been studied. These include the question of maximal non-attacking arrangements of queens on boards of dierent shapes and dimensions, including three-dimensional and toroidal boards. Placements of queens with other pieces or queens on boards with squares removed have been studied, as well as double queen solutions and equivalence classes of solutions with respect to symmetry.

This is just a taste of the history and variation of this interesting problem For more details please check out our reference page.

1.1 Algebraic Representation

Permutations are very natural objects in mathematics and statistics and describe the ways to rearrange $n$ distinct objects. In a classic example, you number the runners in a race with natural numbers from $1$ to $n$ . After the race is run, the resulting order in which the runners finish, $\sigma=(\sigma_1, n_2, n_3, \ldots, n_n)$ , is a permutation of the set $\{1, 2, 3, \ldots, n\}$ . Outcomes of the race and permutations are in one-to-one correspondence and se we see there are always $n!=n(n-1)(n-2)\cdots 2\cdot 1$ possible permutation. Permutations have many representations including one- and two-line notation and as a set of ordered pairs. Each of these are illustrated in our table below.

Permutations are directly connected to $n$ -queens solutions. Solutions to the $n$ -queens problems are a collection of squares from the $n\times n$ chessboard, that is, a solution is a set of ordered pairs of the form $(i,j)$ that indicates the queen is placed on the square in row $i$ and column $j$ . Recall that for a set of queens on a chessboard to be non-attacking, each queen must be on distinct rows and columns. So we have the conditions

Further, a maximum solution always contains $n$ queens so hence we have the numbers $1$ through $n$ appearing exactly once as first coordinates $i_k$ and appearing exactly once as a second coordinate $j_{\ell}$ . This means that $n$ -queens solutions are always permutations and may be written using any permutation representation.

It is not true however that every permutation corresponds to an n-queens solutions. Solutions have the additional condition that no two queens may be on the same diagonal, so

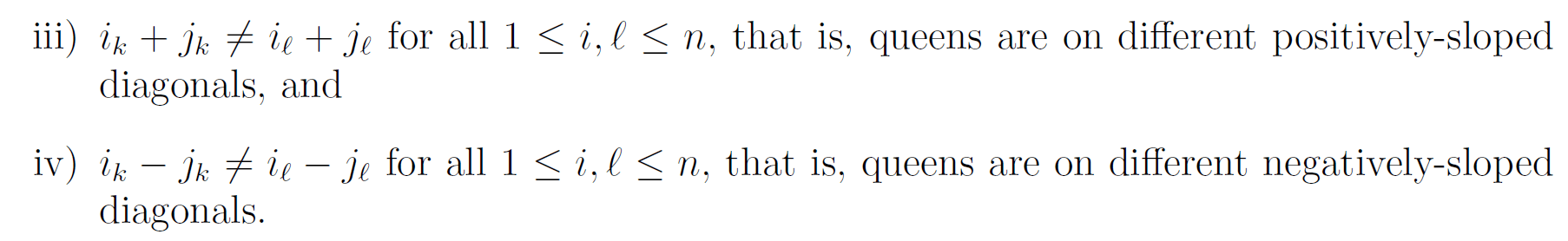
are all distinct.

1.2 Modular Arithmetic Denition

1.3 Constraint Satisfaction Problem

1.4 Maximum Stable Set Problem

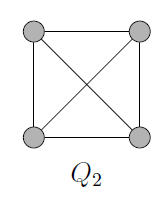
The $n$ -queens problem can also be visualized using graph theory. Very simply, a graph is a collection of vertices along with a set of edges between pairs of these vertices. We can use a $n\times n$ chessboard to create the queen graph denoted $Q_n$ . First, associate each of the $n^2$ squares of the $n\times n$ chessboard with a vertex. Then, draw edges between any two vertices the represent squares on the chessboard from which a queen placed on one square could attack a piece placed on the other square. Practically, this means you have edges between every pair of squares on each diagonal, horizontal, and vertical line. The queen graphs $Q_2$ , $Q_3$ , and $Q_4$ are drawn below.

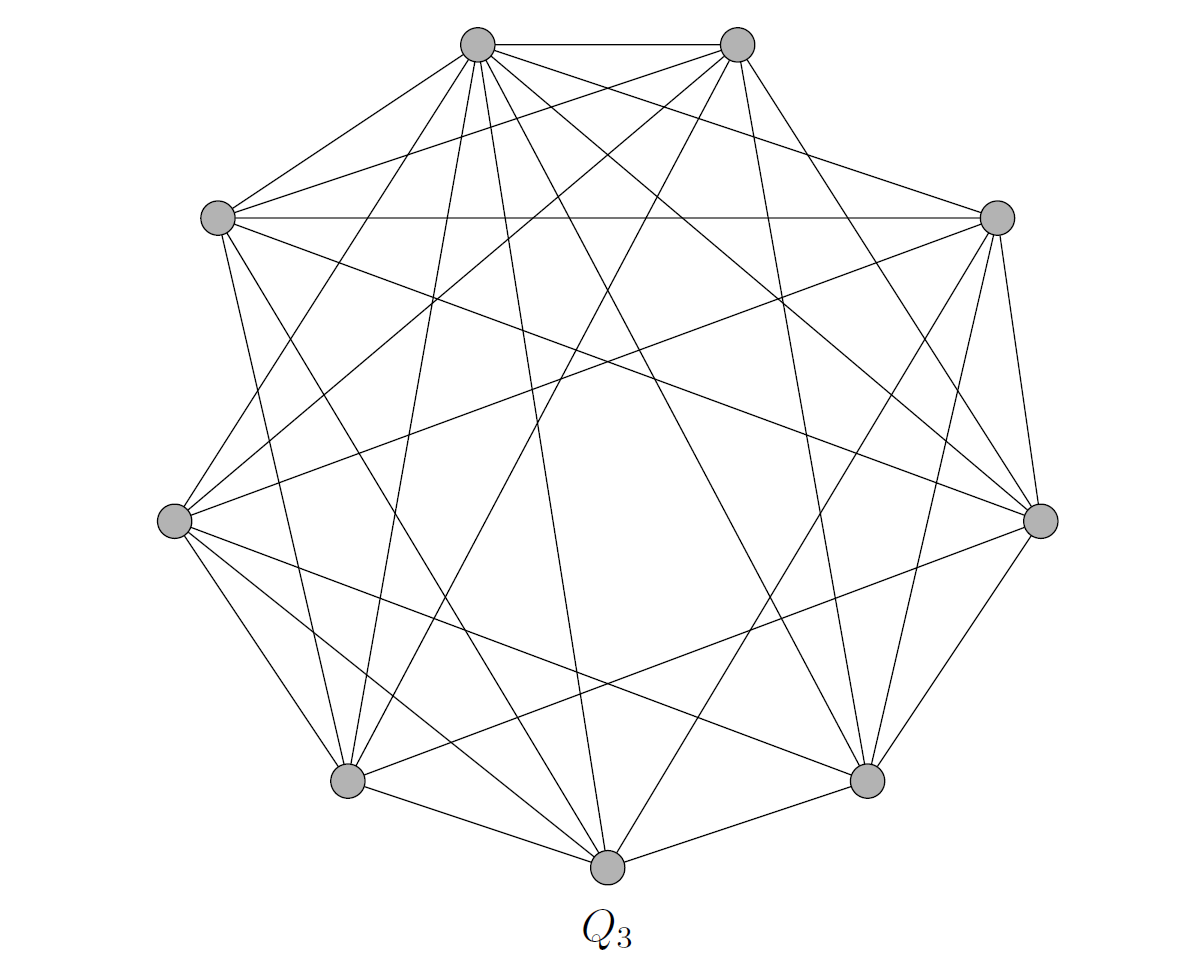
The number of edges in $Q_n$ increases rather quickly. As you can see $Q_2$ has 4 vertices and 6 edges while $Q_3$ has 9 vertices and 28 edges. The next graph in the sequence, $Q_4$ , has 16 vertices and 76 edges. With a little background in combinatorics, it is not too difficult to find a formula for the number of edges and it can be found in sequence A144945 of the OEIS.

Graph theory is concerned with many different properties of graphs, but one is particularly related to the $n$ -queens question. A stable set of vertices in a graph is a set such that no pair of vertices is connected by an edge. The stable set is maximum if it is not contained in any larger stable set. Also known as maximum independent sets, it is common question to ask: what is the size of a maximum stable set? And further, how many maximum stable sets exist?

In the case of the queens graph, any maximum stable set corresponds to a solution to the $n$ -queens problem. This is because each vertex corresponds to a square on the chessboard and stable sets of vertices correspond to sets of squares that cannot be attacked diagonally, horizontally, or vertically. So we may restate the $n$ -queens question as:

Which sets of vertices of the queens graph are maximum stable sets?

In our examples, we can highlight some maximum stable sets. For $n=2$ , because all the vertices are connected, the larges stable set is of size one.

In $Q_3$ , with the exception of the vertex corresponding to the center square in the chessboard, the vertices are each connected to six other vertices. So we choose one of these 8 vertices to start our stable set, and then there are two choices for another vertex to add into the set. In each case, the graph shows that these two vertices are connected, so we can only choose one of them. That means the largest stable set has size 2.

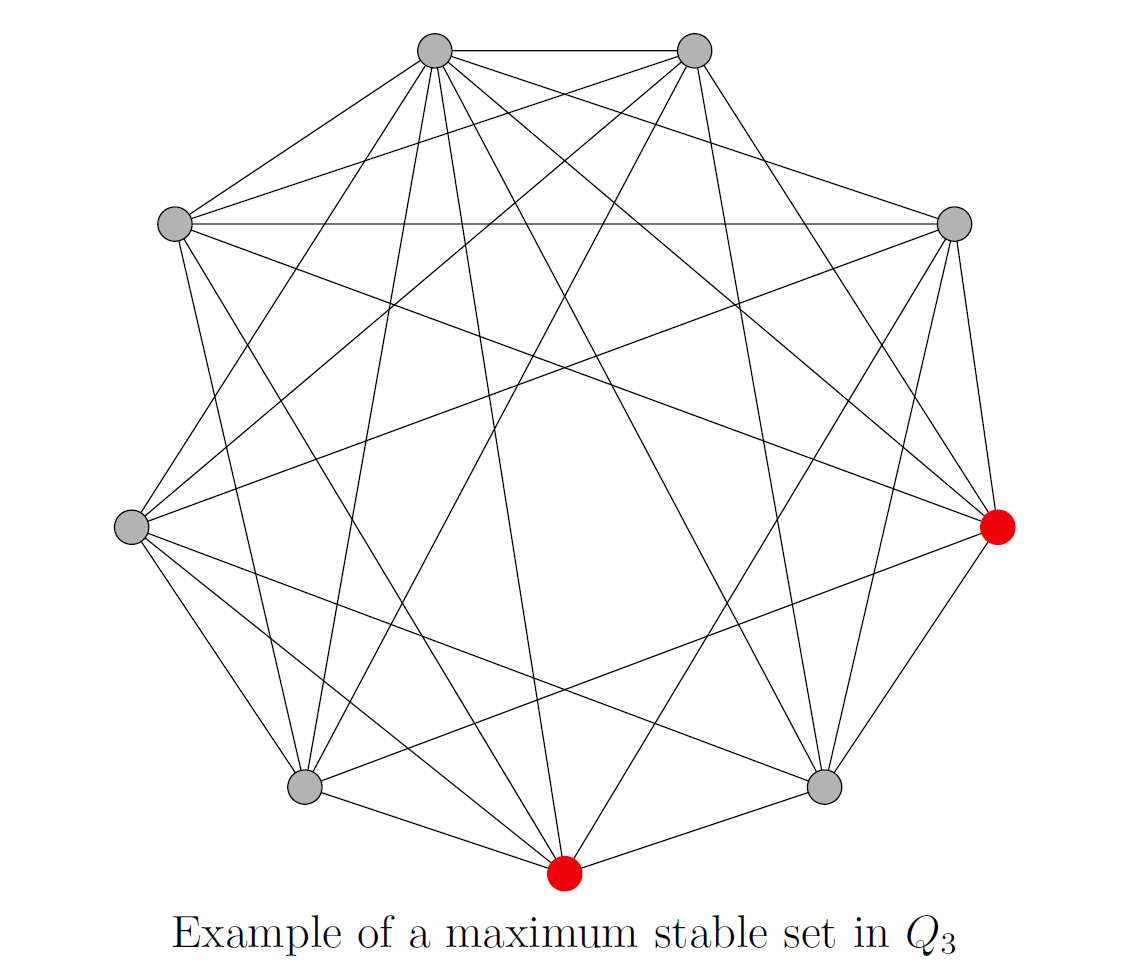
For $Q_4$ , it is starting to get more difficult to read by hand, but we can choose a maximum stable set of size 4 by starting with a vertex connected to eight edges and subsequently adding in three more more non-adjacent vertices.

1.5 Maximum Clique Problem

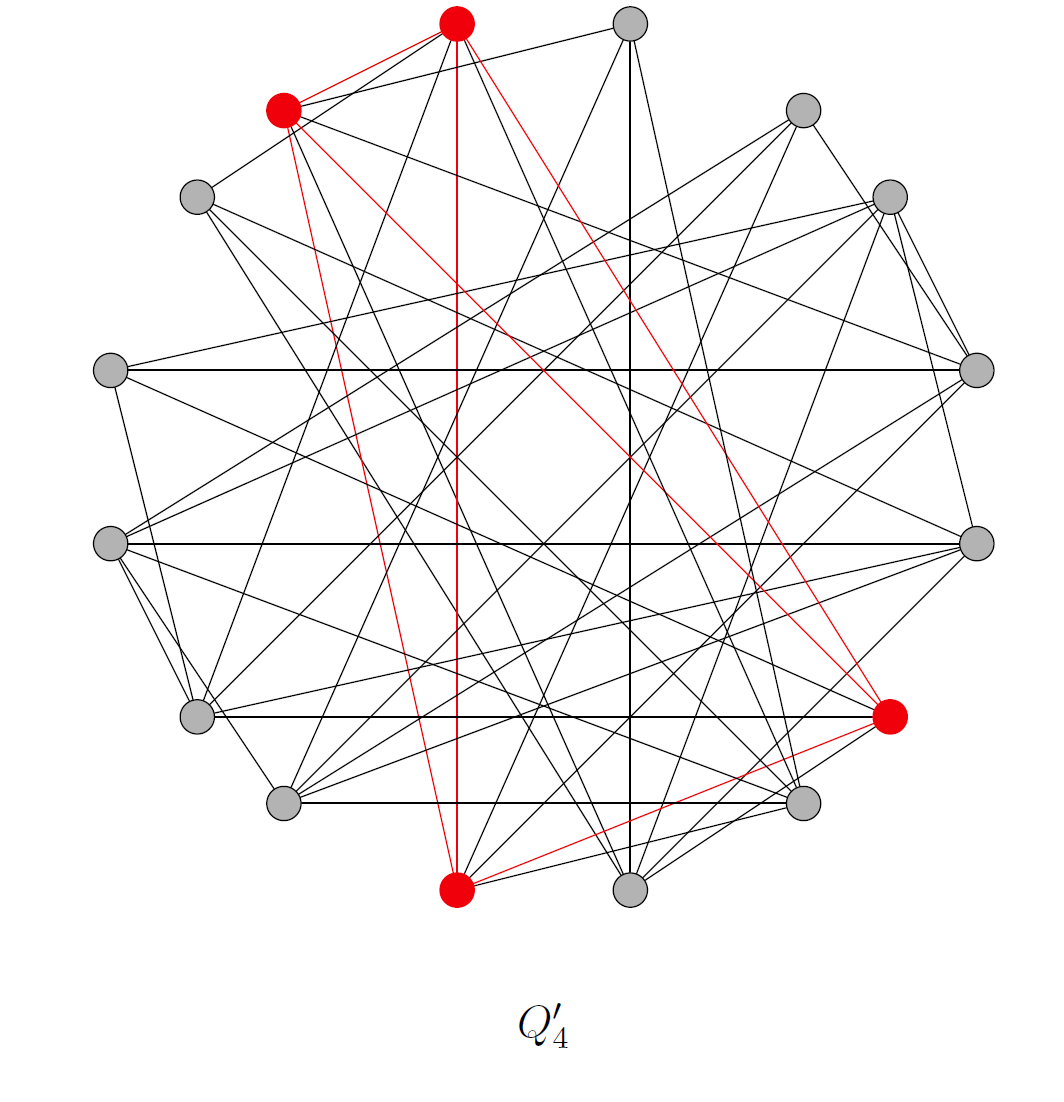
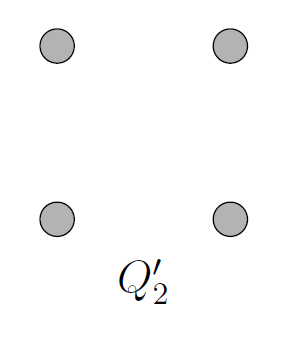
There is another graph visualization for the $n$ -queens problem that utilizes a different graph property. A clique in a graph is a subset of vertices such that every pair of vertices in the subset are connected. Cliques are the opposite extreme of stable sets that have no pair of vertices connected. This time we create a graph using this opposing definition. Let the vertices of the graph correspond to the $n^2$ squares on an $n\times n$ chessboard. Place an edge between a pair of vertices if a queen placed on one of the corresponding squares may not attack the other square, that is, place an edge if the two squares are not along the same diagonal, vertical, or horizontal line on the chessboard. The graphs are the complement of the queens graph. Also called the inverse graph, a complement of a graph in the graph that contains an edge between a pair of vertices if and only if there is not an edge between those vertices in the original graph. We can write $Q_n'$ for the complement of the queens graph $Q_n$ . The complements for $n=2,3,4$ are illustrated below.

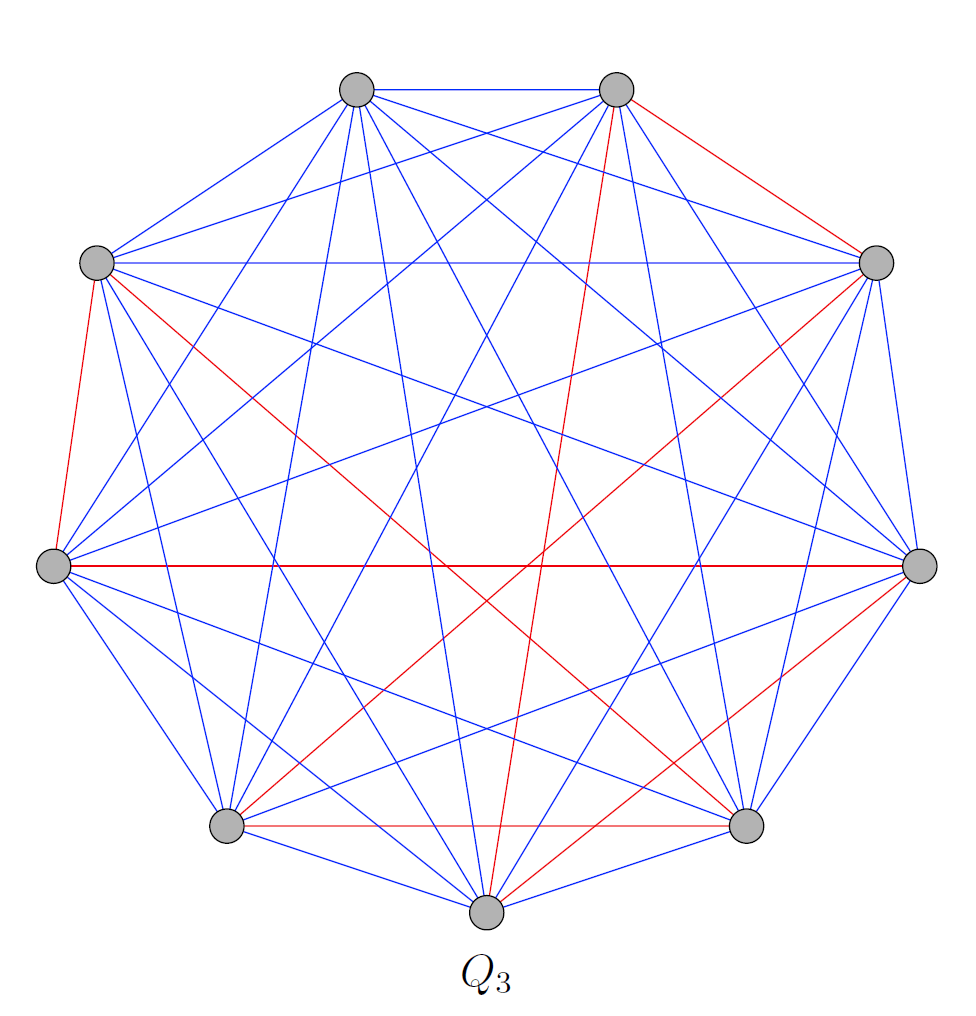
You might note, if you overlay $Q_n'$ with $Q_n$ , you then get the complete graph, $K_n$ , that contains all possible pairs of edges. As an example, $K_3$ is shown below.

Our reformulated $n$ -queens problem is now:

Which sets of vertices in the edge-complement of the queens graph are maximum cliques?

To check for maximum cliques in these graphs, we look for subsets in which all pairs of vertices are connected. You can see that $Q_2$ ‘ has no edges, so the best we can do is to choose a single vertex in four ways. The graph $Q_3$ ‘ has edges which are all 2-cliques, so we want to check if this is maximum. A clique of size three looks like a triangle, so maximum cliques in $Q_3$ ‘ are of size 2 and correspond to the 8 edges. Like in the case of stable sets, as the graph gets bigger, it is more difficult to identify cliques. A clique of size four will probably look like a four-sided polygon with an “X” in the middle. One maximum clique is given below.