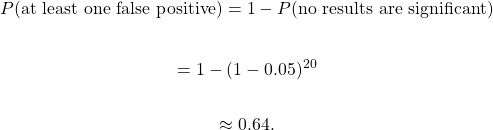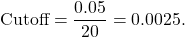Random forests have left the… well, forests of machine learning esoterica and become an analysis technique in nearly every scientific field. In perioperative medicine, this technique has been used to automatically predict patient mortality more accurately than ASA (Hill and colleagues, 2019), blood transfusion needs (Jalali and colleagues 2020), hemorrhage detection (Pinsky and colleagues 2020), and prolonged length of stay (Gabriel and colleagues 2019). But what is a random forest?
Decision tree
To understand the forest, we must first understand the trees. At least, that’s what my meditation app told me this morning. It was a prescient comment because random forests are indeed made up of trees.
Imagine that I asked you if a patient about to undergo surgery is at higher risk of mortality. You might ask me questions like, “What is the patient’s ASA score?” Suppose I say, “2.” Then you might ask about the surgery they’re about to have. Or you might ask me about their age. With each answer, you’re improving your prediction about mortality. And each answer might inform the next question you ask. If I said ASA 3, your second question might be different than if I say ASA 1. Mentally, you are constructing a decision tree to answer my question.
As a visual example, consider if you are trying to decide what kind of room a patient should be placed in based on information from an electrocardiogram. You might use a decision tree like the following.
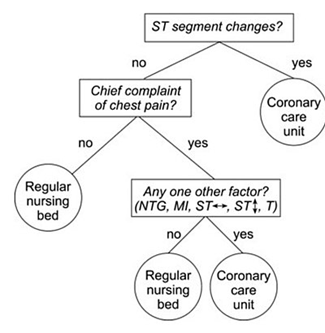
Decision tree example by SilviaCalvanelli. Used with permission under the creative commons CC-BY-SA-4.0 license. This is an illustrative example only. No actionable information is communicated in this figure. It should not be used by anyone for anything.
Now that you have a conceptual understanding of a decision tree, we can return to the idea of random forests.
Random forest
Think about the mortality risk question again. Instead of just asking one clinician, what if I got twenty together in a room and asked them all this question? Obviously, things might get messy if everyone starts asking me about the patient at once. So, in this imaginary scenario, I say that everyone gets to ask one question, and each person must tell me their prediction as soon as their question has been answered. I treat each person’s prediction like a vote, and once all the votes are in, I announce the winning prediction (high risk or not).
With these 20 clinicians each asking one question and getting one vote, I’ve constructed a random forest with 20 trees, each having a maximum depth of 1. If each clinician got to ask 2 questions, then the maximum depth would be 2, and so on. If I had 100 clinicians, then the forest would have 100 trees.
The take away from this example is that a random forest is a whole bunch – potentially thousands – of very simple models that are each allowed to ask only a few questions before making a prediction. The votes from all the simple models are then tallied, and the winning prediction is announced. The technique sometimes seems comically basic, but random forests have proved to be powerful prediction tools.
Notes
The example above certainly isn’t perfect. In a more precise example, the trees wouldn’t directly know each other’s questions, but they would be told whether their answer was improving the prediction based on cases where we already know the right answer, and they would be allowed to change their questions and votes accordingly. This process is called “model training.” Also, each tree wouldn’t start from a place of expert knowledge – like clinicians would – these would be more like randomly selected non-medical folks who were given a list of potential questions to choose from. Finally, the final prediction doesn’t have to be a majority vote. As an alternative, each participating could say how confident they are in their answer, and then the average confidence could be used to pick the winning answer.
References
Hill, B. L., Brown, R., Gabel, E., Rakocz, N., Lee, C., Cannesson, M., Baldi, P., Olde Loohuis, L., Johnson, R., Jew, B., Maoz, U., Mahajan, A., Sankararaman, S., Hofer, I., & Halperin, E. (2019). An automated machine learning-based model predicts postoperative mortality using readily-extractable preoperative electronic health record data. British Journal of Anaesthesia, 123(6), 877–886. https://doi.org/10.1016/j.bja.2019.07.030
Gabriel, R. A., Sharma, B. S., Doan, C. N., Jiang, X., Schmidt, U. H., & Vaida, F. (2019). A Predictive Model for Determining Patients Not Requiring Prolonged Hospital Length of Stay after Elective Primary Total Hip Arthroplasty. Anesthesia and Analgesia, 129(1), 43–50. https://doi.org/10.1213/ANE.0000000000003798
Pinsky, M. R., Wertz, A., Clermont, G., & Dubrawski, A. (2020). Parsimony of hemodynamic monitoring data sufficient for the detection of hemorrhage. Anesthesia and Analgesia, 130(5), 1176–1187.
Jalali, A., Lonsdale, H., Zamora, L. V., Ahumada, L., Nguyen, A. T. H., Rehman, M., Fackler, J., Stricker, P. A., & Fernandez, A. M. (2020). Machine Learning Applied to Registry Data. Anesthesia & Analgesia, Publish Ahead of Print(Xxx), 1–12. https://doi.org/10.1213/ane.0000000000004988